Задание №5. Дискретное косинус-преобразование

Задача является очередным расширением задания №1 и в некоторой степени похожа на задание №3. Нужно реализовать диалог, который будет имитировать JPEG-подобное сжатие изображения. Имитация заключается в том, чтобы показать ожидаемый коэффициент сжатия и картинку с характерными искажениями, но реального сжатия не осуществлять.

Алгоритм

Кодирования

Изображение из RGB переводится в YUV
Каждый канал Y, U, V разбивается на квадратные блоки размера \(8 \times 8\) пикселей (можно \(12 \times 12\) по желанию)
Над каждым блоком проделывается дискретное косинус-преобразование
Результат преобразования квантуется согласно матрице квантования (одна для Y, другая для U, V)
По результатам квантования вычисляется коэффициент сжатия

Декодирования

Результаты квантования умножаются на соответствующий квант согласно матрице квантования
Над каждым блоком проделывается обратное дискретное косинус-преобразование
Из блоков собирается канал Y, U, V
Изображение из YUV переводится в RGB (это и есть измененное изображение, которое нужно показать)

Пусть размер изображения \(w\) на \(h\) пикселей. Если реальные размеры не кратны \(8\) (или \(12\) в случае \(12 \times 12\)), то “лишние” пиксели далее в подсчетах не участвуют. Далее считаем, что размеры изображения кратны размеру блока. Следовательно, размер \(size\) исходного изображения равен \(3 \times w \times h\) байт.

Коэффициент сжатия

Вычисляется как отношение:

\[ratio = \frac{size}{entropy\_size}\]

Размер по энтропии \(entropy\_size\) для всего изображения равен сумме размеров по энтропии каждого канала. Как вычислить размер по энтропии для канала? Берем результат косинус-преобразования для каждого блока и получаем \(64\) (или \(144\) в случае \(12 \times 12\)) числовых последовательности. Каждая последовательность содержит значения из фиксированной позиции в матрице. Например, последовательность из всех коэффициентов в позиции \(\left(0, 0\right)\), т.е. левого верхнего угла матрицы. Для каждой последовательности считается энтропия и умножается на длину последовательности (количество блоков). Полученные результаты суммируются.

Точность вычислений

Все вычисления нужно делать с плавающей точкой (double) и производить округление до целых чисел только там, где это необходимо. Например, преобразование из RGB в YUV нужно делать без округления (значения Y, U и V каналов остаются нецелыми). Результат косинус-преобразования нужно поделить на квант, а только потом округлять до целого числа, которое будет участвовать в подсчете энтропии. В процессе декодирования округлять до целых следует лишь на последнем этапе преобразования из YUV в RGB. При этом нужно не забыть сделать процедуру \(clip\) — значения меньше \(0\) переходят в \(0\), значения больше \(255\) переходят в \(255\).

Преобразование

Пусть \(DCT\) — матрица дискретного косинус-преобразования (является ортогональной), \(DCT^T\) — транспонированная к ней (\(DCT^{-1} = DCT^T\) из-за ортогональности), \(BLOCK\) — матрица с пикселями изображения, \(RESULT\) — результат преобразования. Тогда прямое (direct) преобразование:

\[RESULT = DCT \cdot BLOCK \cdot DCT^T\]

и обратное (inverse) преобразование:

\[BLOCK = DCT^T \cdot RESULT \cdot DCT\]

В матрице \(RESULT\) каждый элемент делится на соответствующий квант из матрицы квантования или сразу зануляется, если в матрице квантования стоит 0.

Общая формула для дискретного косинус-преобразования вектора \(p = \left(p_0, p_1, \ldots, p_{n-1}\right)\) в \(G = \left(G_0, G_1, \ldots, G_{n-1}\right)\):

\[G_f = \sqrt{\frac{2}{n}}C_f \sum_{t=0}^{n-1}p_t \cos\left[\frac{(2t+1)f\pi}{2n}\right], \text{где } C_0 = \frac{1}{\sqrt{2}} \text{ и } C_1, \ldots, C_{n-1} = 1.\]

Обратное преобразование вектора \(G = \left(G_0, G_1, \ldots, G_{n-1}\right)\) в \(p = \left(p_0, p_1, \ldots, p_{n-1}\right)\):

\[p_t = \sqrt{\frac{2}{n}}\sum_{t=0}^{n-1}C_j G_j \cos\left[\frac{(2t+1)j\pi}{2n}\right].\]

В нашем случае преобразуется не вектор, а набор векторов — столбцы матрицы \(BLOCK\). Произведение \(DCT \cdot BLOCK\) дает матрицу, в который каждый столбец является результатом преобразования соответствующего столбца из \(BLOCK\). Далее \(DCT \cdot BLOCK\) подвергается повторному преобразованию, но в качестве векторов уже выступают строки, а не столбцы. Отсюда повторное умножение справа на \(DCT^T\). Дополнительно про матрицу \(DCT\) можно посмотреть, например, в стандарте JPEG, секция A.3.3.

Согласно формулам, приведенным выше, вычисление матрицы \(DCT\) произвольного размера на языке Java:

public static double[][] dct(int size) {
    final double a = Math.sqrt(2.0 / size);
    final double b = Math.PI / (2.0 * size);
    final double c = Math.sqrt(1.0 / size);

    final double[][] m = new double[size][size];
    for (int j = 0; j < size; ++j) {
        m[0][j] = c;
    }

    for (int i = 1; i < size; ++i) {
        for (int j = 0; j < size; ++j) {
      m[i][j] = a * Math.cos(b * (2 * j + 1) * i);
  }
    }

    return m;
}

Интерфейс

Диалог должен позволять задавать обе матрицы квантования (одна для Y, другая для U, V). Каждый элемент меняется в диапазоне от \(0\) до \(200\). Если стоит \(0\), то соответствующий элемент в результирующей матрице зануляется без квантования. Если стоит отличное от \(0\) число, то оно используется в качестве кванта. В диалоге выводится ожидаемый коэффициент сжатия. Примерный внешний вид:

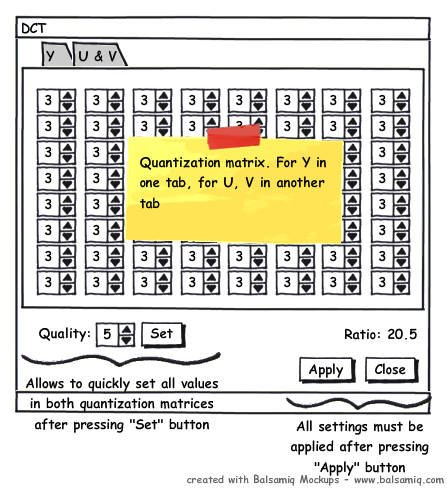
DCT Dialog

В диалоге используется параметр \(Quality\), который позволяет быстро задать все элементы обеих матриц квантования. Делать этом можно любым разумным способом, основанном на следующих утверждениях:

значения квантов должны становиться в целом больше для получения большего коэффициента сжатия,
значения квантов должны становиться больше от левого верхнего угла матрицы (низкие частоты) к правому нижнему (высокие частоты),
значения квантов для U, V должны быть больше, чем для Y при одном и том же значении \(Quality\).

Например, можно воспользоваться формулой \(1 + \left(i + j\right)\cdot Quality\) для получения кванта на месте \(\left(i, j\right)\) в матрице квантования. Если эту формулу использовать для канала Y, то для U, V можно взять \(1 + \left(i + j\right)\cdot \left(Quality + \Delta\right)\), где \(\Delta > 0\). В данном случае, чем больше параметр \(Quality\), тем больше сжатие и меньше реальное качество картинки.